DDP problem of centroidal model. More...

#include <DdpCentroidal.h>

Inheritance diagram for CCC::DdpCentroidal::DdpProblem:

Collaboration diagram for CCC::DdpCentroidal::DdpProblem:

Public Member Functions
EIGEN_MAKE_ALIGNED_OPERATOR_NEW	DdpProblem (double horizon_dt, double mass, const WeightParam &weight_param)
	Constructor. More...

void	setMotionParamFunc (const std::function< MotionParam(double)> &motion_param_func)
	Set function of motion parameter. More...

void	setRefDataFunc (const std::function< RefData(double)> &ref_data_func)
	Set function of reference data. More...

virtual int	inputDim (double t) const override
	Gets the input dimension. More...

virtual StateDimVector	stateEq (double t, const StateDimVector &x, const InputDimVector &u) const override
	Calculate discrete state equation. More...

virtual double	runningCost (double t, const StateDimVector &x, const InputDimVector &u) const override
	Calculate running cost. More...

virtual double	terminalCost (double t, const StateDimVector &x) const override
	Calculate terminal cost. More...

virtual void	calcStateEqDeriv (double t, const StateDimVector &x, const InputDimVector &u, Eigen::Ref< StateStateDimMatrix > state_eq_deriv_x, Eigen::Ref< StateInputDimMatrix > state_eq_deriv_u) const override
	Calculate first-order derivatives of discrete state equation. More...

virtual void	calcStateEqDeriv (double, const StateDimVector &, const InputDimVector &, Eigen::Ref< StateStateDimMatrix >, Eigen::Ref< StateInputDimMatrix >, std::vector< StateStateDimMatrix > &, std::vector< InputInputDimMatrix > &, std::vector< StateInputDimMatrix > &) const override
	Calculate first-order and second-order derivatives of discrete state equation. More...

virtual void	calcRunningCostDeriv (double t, const StateDimVector &x, const InputDimVector &u, Eigen::Ref< StateDimVector > running_cost_deriv_x, Eigen::Ref< InputDimVector > running_cost_deriv_u) const override
	Calculate first-order derivatives of running cost. More...

virtual void	calcRunningCostDeriv (double t, const StateDimVector &x, const InputDimVector &u, Eigen::Ref< StateDimVector > running_cost_deriv_x, Eigen::Ref< InputDimVector > running_cost_deriv_u, Eigen::Ref< StateStateDimMatrix > running_cost_deriv_xx, Eigen::Ref< InputInputDimMatrix > running_cost_deriv_uu, Eigen::Ref< StateInputDimMatrix > running_cost_deriv_xu) const override
	Calculate first-order and second-order derivatives of running cost. More...

virtual void	calcTerminalCostDeriv (double t, const StateDimVector &x, Eigen::Ref< StateDimVector > terminal_cost_deriv_x) const override
	Calculate first-order derivatives of terminal cost. More...

virtual void	calcTerminalCostDeriv (double t, const StateDimVector &x, Eigen::Ref< StateDimVector > terminal_cost_deriv_x, Eigen::Ref< StateStateDimMatrix > terminal_cost_deriv_xx) const override
	Calculate first-order and second-order derivatives of terminal cost. More...

Public Attributes
double	mass_ = 0
	Robot mass [Kg]. More...

Protected Attributes
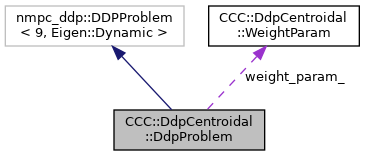
WeightParam	weight_param_
	Weight parameter. More...

std::function< MotionParam(double)>	motion_param_func_
	Function of motion parameter. More...

std::function< RefData(double)>	ref_data_func_
	Function of reference data. More...

Detailed Description

DDP problem of centroidal model.

See stateEq for the state equation of this problem.

Definition at line 87 of file DdpCentroidal.h.

Constructor & Destructor Documentation

◆ DdpProblem()

EIGEN_MAKE_ALIGNED_OPERATOR_NEW CCC::DdpCentroidal::DdpProblem::DdpProblem	(	double	horizon_dt,
		double	mass,
		const WeightParam &	weight_param
	)

inline

Constructor.

Parameters

horizon_dt	discretization timestep in horizon [sec]
mass	robot mass [Kg]
weight_param	objective weight parameter

Definition at line 97 of file DdpCentroidal.h.

Member Function Documentation

◆ calcRunningCostDeriv() [1/2]

virtual void CCC::DdpCentroidal::DdpProblem::calcRunningCostDeriv	(	double	t,
		const StateDimVector &	x,
		const InputDimVector &	u,
		Eigen::Ref< StateDimVector >	running_cost_deriv_x,
		Eigen::Ref< InputDimVector >	running_cost_deriv_u
	)		const

overridevirtual

Calculate first-order derivatives of running cost.

Parameters

t	time [sec]
x	state
u	input
running_cost_deriv_x	first-order derivative of running cost w.r.t. state
running_cost_deriv_u	first-order derivative of running cost w.r.t. input

◆ calcRunningCostDeriv() [2/2]

virtual void CCC::DdpCentroidal::DdpProblem::calcRunningCostDeriv	(	double	t,
		const StateDimVector &	x,
		const InputDimVector &	u,
		Eigen::Ref< StateDimVector >	running_cost_deriv_x,
		Eigen::Ref< InputDimVector >	running_cost_deriv_u,
		Eigen::Ref< StateStateDimMatrix >	running_cost_deriv_xx,
		Eigen::Ref< InputInputDimMatrix >	running_cost_deriv_uu,
		Eigen::Ref< StateInputDimMatrix >	running_cost_deriv_xu
	)		const

overridevirtual

Calculate first-order and second-order derivatives of running cost.

Parameters

t	time [sec]
x	state
u	input
running_cost_deriv_x	first-order derivative of running cost w.r.t. state
running_cost_deriv_u	first-order derivative of running cost w.r.t. input
running_cost_deriv_xx	second-order derivative of running cost w.r.t. state
running_cost_deriv_uu	second-order derivative of running cost w.r.t. input
running_cost_deriv_xu	second-order derivative of running cost w.r.t. state and input

◆ calcStateEqDeriv() [1/2]

virtual void CCC::DdpCentroidal::DdpProblem::calcStateEqDeriv	(	double	t,
		const StateDimVector &	x,
		const InputDimVector &	u,
		Eigen::Ref< StateStateDimMatrix >	state_eq_deriv_x,
		Eigen::Ref< StateInputDimMatrix >	state_eq_deriv_u
	)		const

overridevirtual

Calculate first-order derivatives of discrete state equation.

Parameters

t	time [sec]
x	state
u	input
state_eq_deriv_x	first-order derivative of state equation w.r.t. state
state_eq_deriv_u	first-order derivative of state equation w.r.t. input

The first-order derivative of the discrete state equation is expressed as follows.

\begin{align*} \frac{\partial \boldsymbol{x}_{k+1}}{\partial \boldsymbol{x}_k} &= \begin{bmatrix} \boldsymbol{O} & \dfrac{1}{m} \boldsymbol{I} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{O} & \boldsymbol{O} \\ (\sum_i \lambda_i \boldsymbol{\rho}_i) \times & \boldsymbol{O} & \boldsymbol{O} \end{bmatrix} \Delta t + \boldsymbol{I} \\ \frac{\partial \boldsymbol{x}_{k+1}}{\partial \boldsymbol{u}_k} &= \begin{bmatrix} \cdots & \boldsymbol{O} & \cdots \\ \cdots & \boldsymbol{\rho}_i & \cdots \\ \cdots & (\boldsymbol{p}_i - \boldsymbol{c}) \times \boldsymbol{\rho}_i & \cdots \end{bmatrix} \Delta t \end{align*}

◆ calcStateEqDeriv() [2/2]

virtual void CCC::DdpCentroidal::DdpProblem::calcStateEqDeriv	(	double	,
		const StateDimVector &	,
		const InputDimVector &	,
		Eigen::Ref< StateStateDimMatrix >	,
		Eigen::Ref< StateInputDimMatrix >	,
		std::vector< StateStateDimMatrix > &	,
		std::vector< InputInputDimMatrix > &	,
		std::vector< StateInputDimMatrix > &
	)		const

inlineoverridevirtual

Calculate first-order and second-order derivatives of discrete state equation.

Parameters

t	time [sec]
x	state
u	input
state_eq_deriv_x	first-order derivative of state equation w.r.t. state
state_eq_deriv_u	first-order derivative of state equation w.r.t. input
state_eq_deriv_xx	second-order derivative of state equation w.r.t. state
state_eq_deriv_uu	second-order derivative of state equation w.r.t. input
state_eq_deriv_xu	second-order derivative of state equation w.r.t. state and input

Definition at line 217 of file DdpCentroidal.h.

◆ calcTerminalCostDeriv() [1/2]

virtual void CCC::DdpCentroidal::DdpProblem::calcTerminalCostDeriv	(	double	t,
		const StateDimVector &	x,
		Eigen::Ref< StateDimVector >	terminal_cost_deriv_x
	)		const

overridevirtual

Calculate first-order derivatives of terminal cost.

Parameters

t	time [sec]
x	state
terminal_cost_deriv_x	first-order derivative of terminal cost w.r.t. state

◆ calcTerminalCostDeriv() [2/2]

virtual void CCC::DdpCentroidal::DdpProblem::calcTerminalCostDeriv	(	double	t,
		const StateDimVector &	x,
		Eigen::Ref< StateDimVector >	terminal_cost_deriv_x,
		Eigen::Ref< StateStateDimMatrix >	terminal_cost_deriv_xx
	)		const

overridevirtual

Calculate first-order and second-order derivatives of terminal cost.

Parameters

t	time [sec]
x	state
terminal_cost_deriv_x	first-order derivative of terminal cost w.r.t. state
terminal_cost_deriv_xx	second-order derivative of terminal cost w.r.t. state

◆ inputDim()

virtual int CCC::DdpCentroidal::DdpProblem::inputDim ( double t ) const

overridevirtual

Gets the input dimension.

Parameters

t time

◆ runningCost()

virtual double CCC::DdpCentroidal::DdpProblem::runningCost	(	double	t,
		const StateDimVector &	x,
		const InputDimVector &	u
	)		const

overridevirtual

Calculate running cost.

Parameters

t	time [sec]
x	current state \(\boldsymbol{x}_k\)
u	current input \(\boldsymbol{u}_k\)

Returns: running cost \(L_k\)

◆ setMotionParamFunc()

void CCC::DdpCentroidal::DdpProblem::setMotionParamFunc ( const std::function< MotionParam(double)> & motion_param_func )

inline

Set function of motion parameter.

Parameters

motion_param_func function of motion parameter

Definition at line 105 of file DdpCentroidal.h.

◆ setRefDataFunc()

void CCC::DdpCentroidal::DdpProblem::setRefDataFunc ( const std::function< RefData(double)> & ref_data_func )

inline

Set function of reference data.

Parameters

ref_data_func function of reference data

Definition at line 113 of file DdpCentroidal.h.

◆ stateEq()

virtual StateDimVector CCC::DdpCentroidal::DdpProblem::stateEq	(	double	t,
		const StateDimVector &	x,
		const InputDimVector &	u
	)		const

overridevirtual

Calculate discrete state equation.

Parameters

t	time [sec]
x	current state \(\boldsymbol{x}_k\)
u	current input \(\boldsymbol{u}_k\)

Returns: next state \(\boldsymbol{x}_{k+1}\)

Dynamics is expressed by the following equation.

\begin{align*} \boldsymbol{\dot{P}} &= \sum_i \lambda_i \boldsymbol{\rho}_i - m \boldsymbol{g} \\ \boldsymbol{\dot{L}} &= \sum_i (\boldsymbol{p}_i - \boldsymbol{c}) \times \lambda_i \boldsymbol{\rho}_i \end{align*}

\(\boldsymbol{c}\), \(\boldsymbol{P}\), and \(\boldsymbol{L}\) are CoM, linear momentum, and angular momentum, respectively. \(\boldsymbol{p}_i\), \(\lambda_i\), and \(\boldsymbol{\rho}_i\) are position, force scale, and ridge vector of i-th contact vertex ridge, respectively.

This can be represented as a nonlinear system as follows.

\begin{align*} \boldsymbol{\dot{x}} &= \begin{bmatrix} \dfrac{1}{m} \boldsymbol{P} \\ \sum_i \lambda_i \boldsymbol{\rho}_i - m \boldsymbol{g} \\ \sum_i (\boldsymbol{p}_i - \boldsymbol{c}) \times \lambda_i \boldsymbol{\rho}_i \end{bmatrix} \end{align*}

State and control input are expressed by the following equations.

\begin{align*} \boldsymbol{x} = \begin{bmatrix} \boldsymbol{c} \\ \boldsymbol{P} \\ \boldsymbol{L} \end{bmatrix}, \boldsymbol{u} = \begin{bmatrix} \vdots \\ \lambda_i \\ \vdots \end{bmatrix} \end{align*}

Euler method is used to discretize the system.

\begin{align*} \boldsymbol{x}_{k+1} = \boldsymbol{\dot{x}}_{k} \Delta t + \boldsymbol{x}_{k} \end{align*}

◆ terminalCost()

virtual double CCC::DdpCentroidal::DdpProblem::terminalCost	(	double	t,
		const StateDimVector &	x
	)		const

overridevirtual

Calculate terminal cost.

Parameters

t	time [sec]
x	current state \(\boldsymbol{x}_k\)

Returns: terminal cost \(\phi_k\)

Member Data Documentation

◆ mass_

double CCC::DdpCentroidal::DdpProblem::mass_ = 0

Robot mass [Kg].

Definition at line 284 of file DdpCentroidal.h.

◆ motion_param_func_

std::function<MotionParam(double)> CCC::DdpCentroidal::DdpProblem::motion_param_func_

protected

Function of motion parameter.

Definition at line 291 of file DdpCentroidal.h.

◆ ref_data_func_

std::function<RefData(double)> CCC::DdpCentroidal::DdpProblem::ref_data_func_

protected

Function of reference data.

Definition at line 294 of file DdpCentroidal.h.

◆ weight_param_

WeightParam CCC::DdpCentroidal::DdpProblem::weight_param_

protected

Weight parameter.

Definition at line 288 of file DdpCentroidal.h.

The documentation for this class was generated from the following file:

/home/runner/work/CentroidalControlCollection/CentroidalControlCollection/colcon_ws/src/isri-aist/CentroidalControlCollection/include/CCC/DdpCentroidal.h

Public Member Functions

Public Attributes

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

◆ DdpProblem()

Member Function Documentation

◆ calcRunningCostDeriv() [1/2]

◆ calcRunningCostDeriv() [2/2]

◆ calcStateEqDeriv() [1/2]

◆ calcStateEqDeriv() [2/2]

◆ calcTerminalCostDeriv() [1/2]

◆ calcTerminalCostDeriv() [2/2]

◆ inputDim()

◆ runningCost()

◆ setMotionParamFunc()

◆ setRefDataFunc()

◆ stateEq()

◆ terminalCost()

Member Data Documentation

◆ mass_

◆ motion_param_func_

◆ ref_data_func_

◆ weight_param_